Geometric Progression Sum to Infinity

Sum to infinity for Geometric Series Unlike with. Feel free to w.

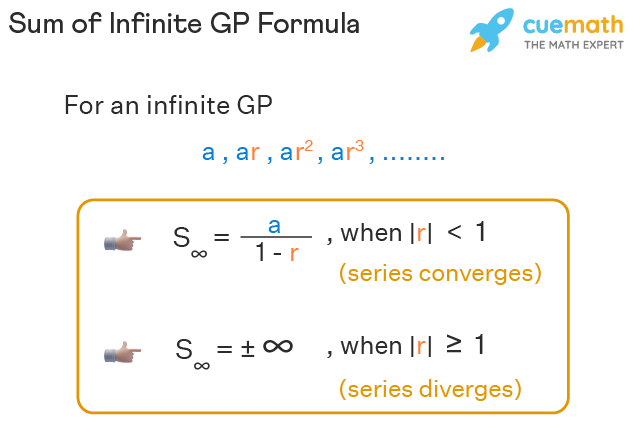
Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp

S n 1 r a 1 r n.

. Sum of Infinite Geometric Progression IGP The number of terms in infinite geometric progression will approach to infinity n. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. Only the range -10 r 0 10 can be used to define the sum of infinite geometric progression.

In this video I will show you a simple example on how to calculate the sum to infinity of geometric progressions by appling the formula. In this video we will discuss infinite geometric series or sum to infinity. Subscribe for more math t.

Derivation of the formula to find the sum of an infinite Geometrical Progression where common ratio is an proper fractionFor more videos on this topic visi. I know that the geometric distribution follows the rules of a geometric progression thus by using the sum to infinity formula which I know its proof and is really convinced by it a 1 r We can. We will derive the formula in finding the sum of the terms of infinite geometric.

The sum of the infinite geometric Progression Formula is divergent. Hence obtaining S n a 1 r n 1 r as required by dividing both sides by 1 r. The formula for the sum of an infinite geometric series with first term a and common ratio r is a 1 - r 256 1 - 14 10243.

Sum of infinite geometric progression can only. In an infinite geometric progression aarar2ar3 ldots ldots infty the formula used to find the sum of terms in an infinite. The procedure to use the infinite geometric series calculator is as follows.

Now click the button Calculate to. A Level Pure This video explains how the sum to infinity of a geometric series is derived and how to calculate the sum to infinity. Tutorial on Geometric series.

Promoted by The Penny Hoarder. In an infinite geometric progression the number of terms approaches infinity n. Sum of Infinite Geometric Series.

Enter the first term and common ratio in the respective input field. We then factorise to get. For example the series is geometric because.

This is a sequence in which each term consists of the product of an arithmetic progression and a geometric progression. The concept of infinite geometric progression means a GP that can extend to infinity. The series of numbers where the ratio of any two consecutive terms is the same is called a Geometric Progression.

In variables it looks like.

Proof Of The Geometric Series Formula Finite Infinite Youtube

Finding The Sum Of An Infinite Geometric Series Youtube

Geometric Series Sum To Infinity Examsolutions Youtube

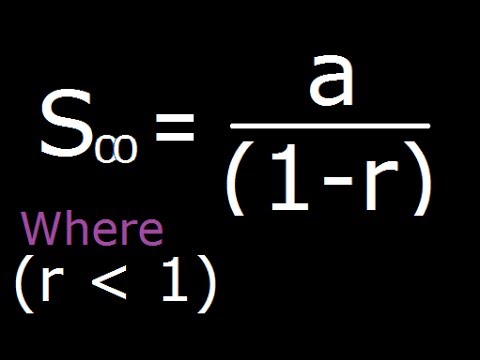
Geometrical Progression Sum Of Infinite Terms Derivation Youtube